1. Introduction
We will discuss decentralization of Bitcoin in this post. The scheme is first proposed in the whitepaper published by Satoshi. In peer-to-peer cryptocurrency systems, lots of obstacles arise compared to centralised systems such as latency of network, double-spend-attack, loss of data etc. Because of those constraints, Bitcoin does not purely rely on technical methods to achieve decentralisation, but it’s a combination of technical methods and clever incentive engineering. In this post, we first give the simplied protocol Bitcoin used and then elaborate on this protocol.
2. Distributed consensus protocol
Imagine you’re in charge of the backend for a large social networking company like Facebook. Systems of this sort typically have thousands or even millions of servers, which together form a massive distributed database that records all of the actions that happen in the system. Each piece of information must be recorded on several different nodes in this backend, and the nodes must be in sync about the overall state of the system. Thus, a consensus protocol is needed in this context. A distributed consensus protocol should have two properties as discussed below:
Distributed consensus protocol: There are n nodes that each have an input value. Some of these nodes are faulty or malicious. A distributed consensus protocol has the following two properties:
-
It must terminate with all honest nodes in agreement on the value
-
The value must have been generated by an honest node
Thus, distributed consensus protocol plays a central role in the design of distributed systems. However, the lack of global time heavily constrains the set of algorithms that can be used in the consensus protocols. In fact, because of these constraints, much of the literature on distributed consensus is somewhat pessimistic, and many impossibility results have been proven. One very well known impossibility result is the Byzantine Generals Problem.
2.1 Blockchain protocol
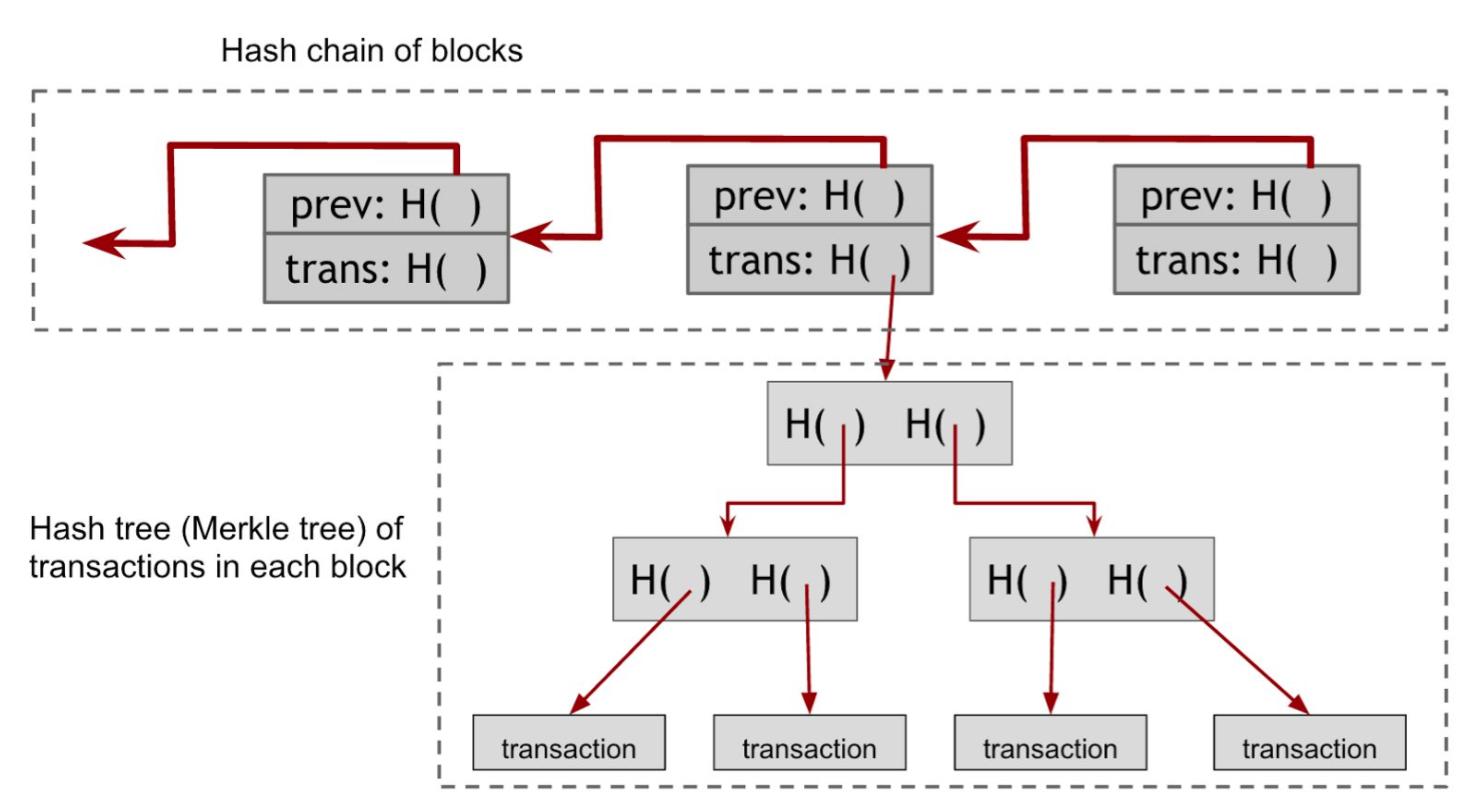
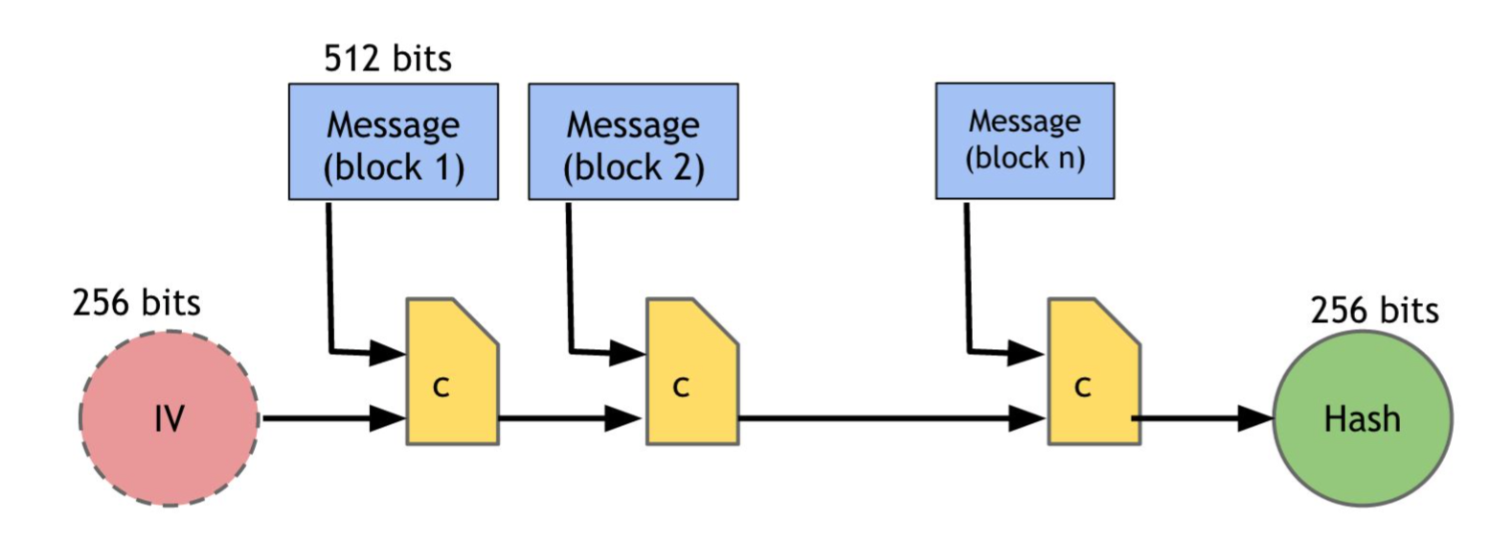
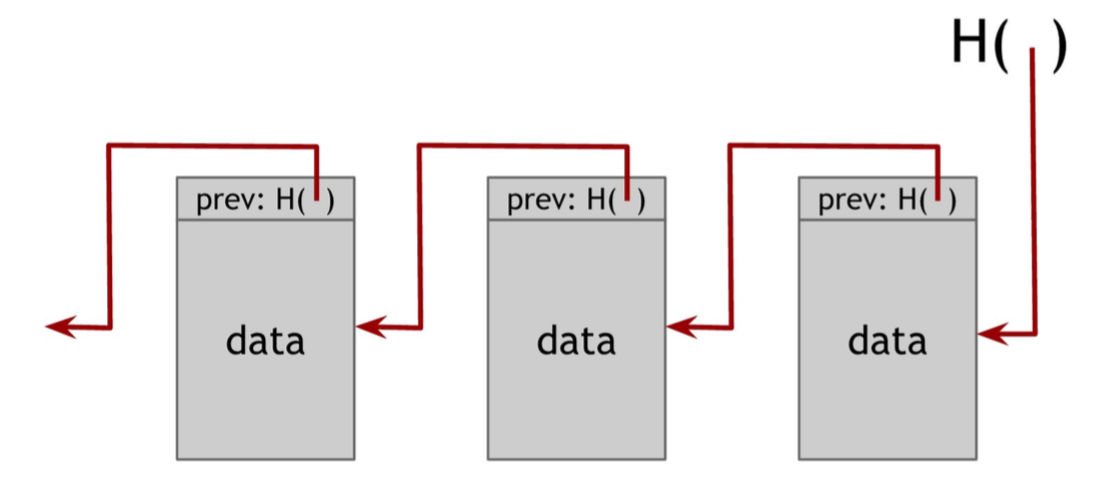
Bitcoin uses Blockchain to record the transactions. Thus, Blockchain needs protocol to sync the blocks for nodes in the network. Suppose there is somehow an ability to pick a random node in the system (in Bitcoin, this random node is picked by a procedure called mining), this node gets to propose the next block in the chain. Here is the simplified protocol.
Bitcoin consensus algorithm (simplified)
This algorithm is simplified in that it assumes the ability to select a random node in a manner that is not vulnerable to Sybil attacks.
-
New transactions are broadcast to all nodes
-
Each node collects new transactions into a block
-
In each round a random node gets to broadcast its block
-
Other nodes accept the block only if all transactions in it are valid (unspent, valid signatures)
-
Nodes express their acceptance of the block by including its hash in the next block they create
By this manner, the system is robust enough to prevent potential attacks which we will talk about later. First, we will talk about how other nodes process the block they received a block(step 4 and step 5).
2.1.1 Receive block
When receiving a new block message broadcasted from step 3, the node should extend the blockchain they are maintaining. There are three kinds of blocks in the blockchain:
-
blocks in the main branch. The transactions in these blocks are considered at least tentatively confirmed
-
blocks on side branches off the main branch. These blocks have at least tentatively lost the race to be in the main branch
-
orphan blocks. These are blocks which don’t link into the main branch, normally because of a missing predecessor or nth-level predecessor.
The largest branch in the blockchain is called the main branch. When receiving a new block, the node will try to add this into main branch, side branches or orphan block pool depending on the hash pointer. After adding it, three cases will arise:
-
block further extends the main branch;
-
block extends a side branch but does not add enough difficulty to make it become the new main branch;
-
block extends a side branch and makes it the new main branch.
Depending on which case happens, the blockchain takes different actions. An overview of the actions is available at protocol.
2.1.2 Advantages
The protocol can prevent many kinds of attacks. Let’s now try to understand why this consensus algorithm works. To do this, let’s consider how a malicious adversary — who we’ll call Alice — may be able to subvert this process.
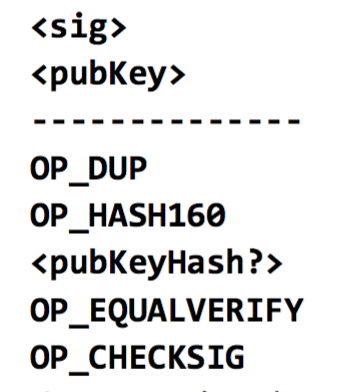
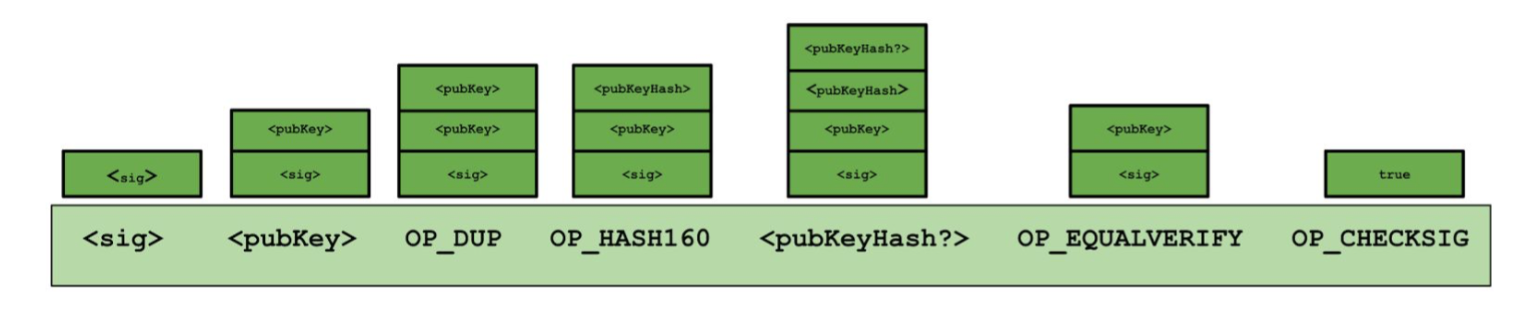
Stealing Bitcoins. Can Alice simply steal bitcoins belonging to another user at an address she doesn’t control? No. Even if it is Alice’s turn to propose the next block in the chain, she cannot steal other users’ bitcoins. Doing so would require Alice to create a valid transaction that spends that coin. This would require Alice to forge the owners’ signatures which she cannot do if a secure digital signature scheme is used. So as long as the underlying cryptography is solid, she’s not able to simply steal bitcoins.
Denial of service attack. Let’s consider another attack. Say Alice really dislikes some other user Bob. Alice can then decide that she will not include any transactions originating from Bob’s address in any block that she proposes to get onto the block chain. In other words, she’s denying service to Bob. While this is a valid attack that Alice can try to mount, luckily it’s nothing more than a minor
annoyance. If Bob’s transaction doesn’t make it into the next block that Alice proposes, he will just wait until an honest node gets the chance to propose a block and then his transaction will get into that block. So that’s not really a good attack either.
Double-spend attack. Let’s assume that Alice is a customer of some online merchant or website run by Bob, who provides some online service in exchange for payment in bitcoins. Let’s say Bob’s service allows the download of some software. So here’s how a double-spend attack might work. Alice adds an item to her shopping cart on Bob’s website and the server requests payment. Then Alice creates a Bitcoin transaction from her address to Bob’s and broadcasts it to the network. Let’s say that some honest node creates the next block, and includes this transaction in that block. So there is now a block that was created by an honest node that contains a transaction that represents a payment from Alice to the merchant Bob. The graph below shows the effect to Blockchain.
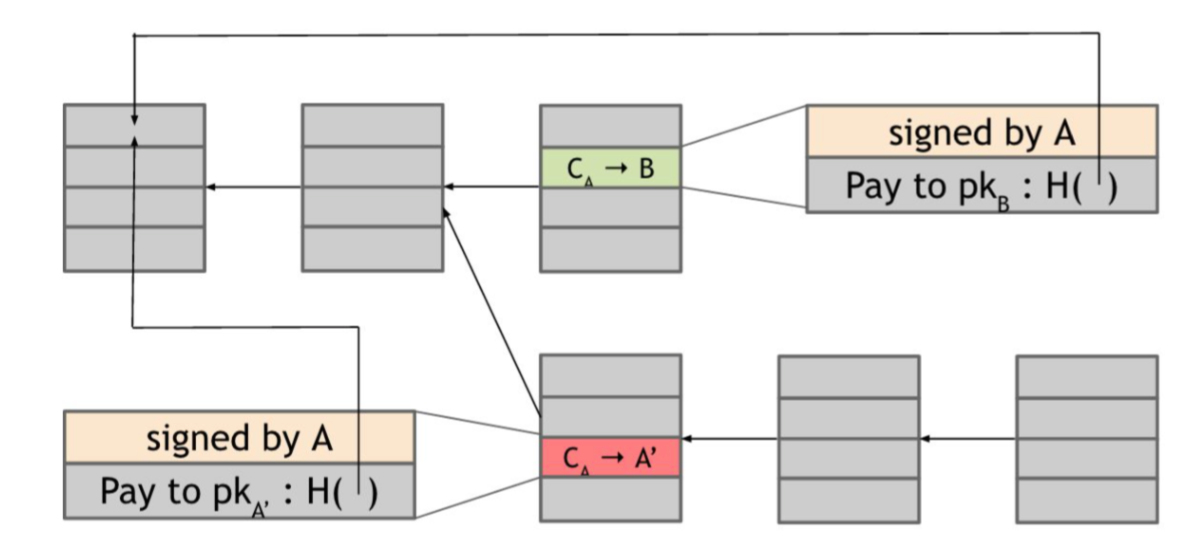
And how do we know if this double spend attempt is going to succeed or not? Well, that depends on which block will ultimately end up on the long-term consensus chain — the one with the Alice → Bob transaction or the one with the Alice → Alice transaction. What determines which block will be included? Honest nodes follow the policy of extending the longest valid branch, so which branch will they extend? There is no right answer! At this point, the two branches are the same length — they only differ in the last block and both of these blocks are valid. The node that chooses the next block then may decide to build upon either one of them. Thus, only one of two transactions will finally be kept in the blockchain. Alice cannot achieve double-spend attack in this context. The merchart Bob can wait confirmations for transactions to decide whether let Alice download the software. Thus, the protocol can prevent double-spend attack.
3. Pick up a random node
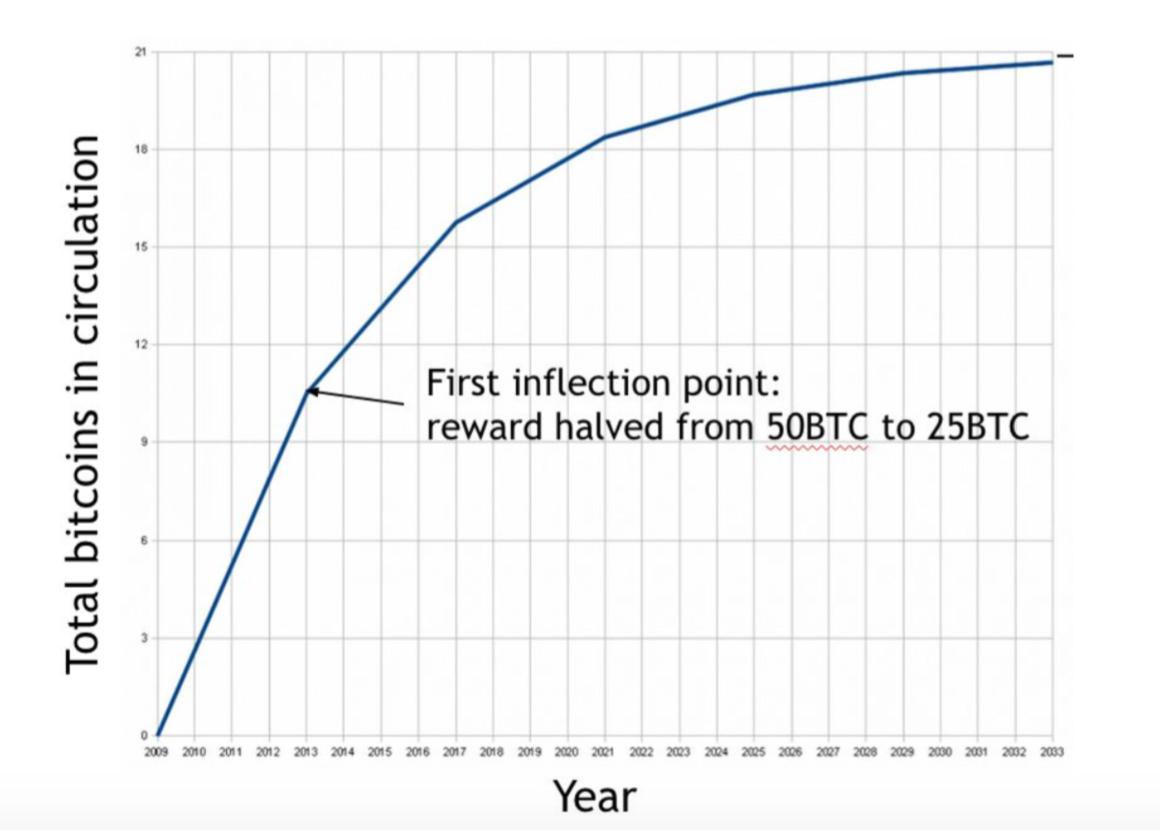
In this section, we will talk about how to randomly choose a node from the network. Nodes in the network are rewarded by being chosen as this node. Thus, this motivates people to get the opportunity for being chosen through ‘mining’. The rewards include the creation of new coins and transaction fees. At the time of this writing, the value of the block reward is fixed at 25 Bitcoins. But it actually halves every 210,000 blocks. Based on the rate of block creation that we will see shortly, this means that the rate drops roughly every four years (because in expection, a new block is generated every 10 minutes). We’re now in the second period. For the first four years of Bitcoin’s existence, the block reward was 50 bitcoins; now it’s 25. The node chosen will get 25 newly created Bitcoins.
Now, we introduce how the node is chosen through ‘mining’. The node is chosen through proof-of-work. The key idea behind proof-of-work is that we approximate the selection of a random node by instead selecting nodes in proportion to a resource that we hope that nobody can monopolize. If, for example, that resource is computing power, then it’s a proof-of-work system.
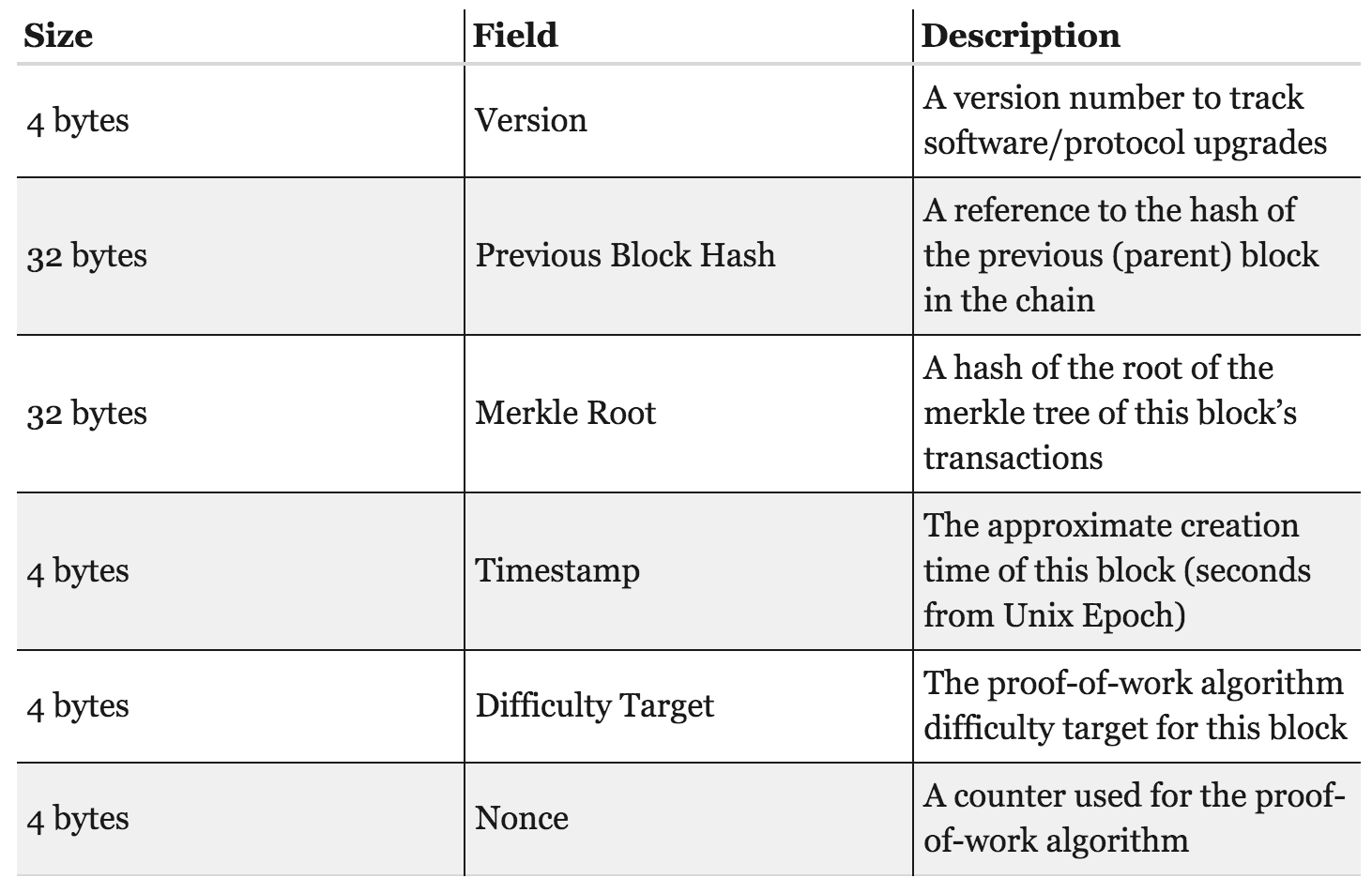
Bitcoin achieves proof-of-work using hash puzzles. In order to create a block, the node that proposes that block is required to find a number, or nonce, such that when you concatenate the nonce, the previous hash, and the list of transactions that comprise that block and take the hash of this whole string, then that hash output should be a number that falls into a target space that is quite small in relation to the much larger output space of that hash function. We can define such a target space as any value falling below a certain target value. In this case, the nonce will have to satisfy the inequality:
H(nonce || prev_hash || tx || tx || ... || tx) < target.
The first node which finds this nonce proposes the block. Thus, in order to be chosen, the node should have a great computing power. The incentive to get Bitcoins flourishes the Bitcoin mining industry.
This post introduces how Bitcoin achieves concensus and how to choose random node to propose next block. In next post, we will introduce the data format of blocks.


 To view the real transactions happening in Bitcoin network, some websites can be referred to such as
To view the real transactions happening in Bitcoin network, some websites can be referred to such as